Search
NMR Application: Education

A solid understanding of NMR spectroscopy is a basic learning goal for any student of chemistry. The hands-on approach to learning is the most powerful method for instructors in both classroom settings and in the teaching laboratory. Direct experience with acquiring and processing NMR spectra to determine product purity or to monitor the course of a chemical reaction is extremely valuable, especially for organic chemistry students.
The challenges for teaching modern NMR techniques are manifold:
- Accessing modern high-field research NMR facilities for student instruction
- Managing complex and technically challenging instrumental operations
- Funding expensive equipment dedicated solely to teaching
- Housing oversized instrumentation in existing lab space
- Developing NMR applications to complement existing lab curricula
- Allowing undergraduate chemistry students direct access to an expensive instrument
- Gaining or maintaining ACS or other national accreditation by incorporating NMR into the curriculum.
The Thermo Scientific picoSpin NMR spectrometer offers solutions to these challenges:
- Compact, lightweight design, without requirements for liquid cryogens or other special facilities
- Easily fits on laboratory bench tops, is conveniently stored, and can be relocated as needed
- Capillary design, easy-to-shim permanent magnet and simple software interface dispense with complicated initialization and operation procedures
- Chemistry students can acquire their own spectra in the lab
- Instructors can focus on NMR applications rather than the technical aspects of instrument operation
- Low purchase and operational costs
- Ideal for routine identification of reaction mixtures and crude or purified products at the lab bench
- Lab procedures are easily adapted to take advantage of both qualitative and quantitative techniques.
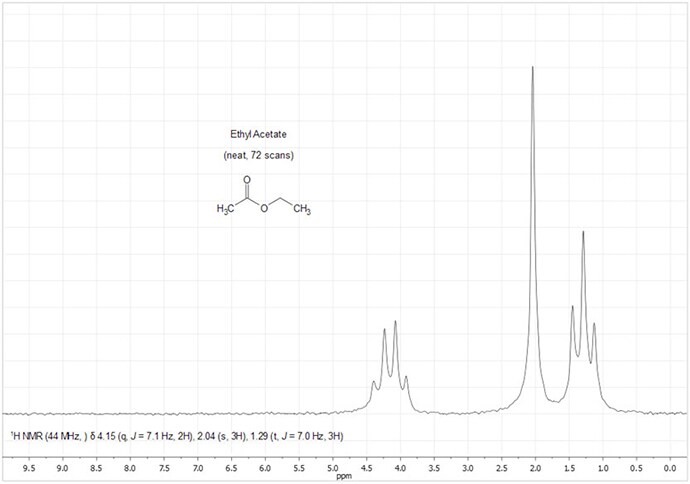
The 1H NMR spectrum of ethyl acetate shows three individual signals due to three different hydrogen environments. The protons of the aceyl methyl group H3C(C=O) appear up field with a chemical shift value of 2.04 ppm. These protons experience no spin-spin coupling, and thus appear as a single peak with a weight of 3. Protons of the ethyl group experience two different chemical environments. Methylene protons (-CH2-) attached to the more electronegative oxygen are deshielded and shifted down field to 4.12 ppm with a peak integral of 2. The methyl protons (-CH3) of the ethyl moiety are the most shielded and appear farthest up field at 1.26 ppm with a peak integral of 3. Asymmetry in the ethyl group results in vicinal coupling of the terminal methyl (-CH3) protons to the methylene (-CH2-) protons, yielding a simple first-order splitting pattern with expected multiplicities of a triplet and quartet. The -CH2- proton signal is split into a quartet (δ4.12) by the three neighboring methyl protons, and the –CH3 proton signal is split into a triplet (δ1.26) due to the two adjunct methylene protons. This splitting pattern is unmistakable and easily resolved by the picoSpin 45 spectrometer.
Education applications
13C Satellites
Direct 13C-1H coupling can be observed in 1H spectra for molecular systems of high molecular symmetry and which have magnetically equivalent protons. The presence 13C breaks this symmetry, allowing spin-spin interaction between 1H and 13C nuclei between directly bonded atoms to be observed even when only a natural abundance (1.1%) of 13C is available in the molecule. This hetero-nuclear coupling effect is best observed in pure liquid samples, high concentration solutions, or doped solutions, using both high and low dielectric solvents and dopants.
The magnitude of the 13C-1H coupling constant (JCH) shows a direct dependence on the amount of s character in the bond between directly bonded nuclei and, hence, is a reflection of the hybridization and bond length. Typically, JCH values for sp3 hybridization fall in the 120-130 Hz range and will depend on the degree of bond polarization, for sp2 hybridization JCH values range from 150-175 Hz, and for sp hybridization JCH values are as high as 250 Hz. Long range 1H-C-13C are much smaller, J~3-4 Hz, and more difficult to observed directly.
Thermo Scientific™ picoSpin™ NMR spectra acquired from a variety of high molecular symmetry molecules where 13C satellite peaks have been observed are presented below. In each case an observed JCH coupling constant of ~125 Hz is consistent with an sp3 hybridized H-C bond.




Thermo Scientific™ picoSpin™ 45 NMR spectra acquired from the 50% (v/v) solutions of the butanol series of regioisomers, 1-butanol (CHCl3), 2-butanol (acetone), isobutanol (acetone), and t-butanol (CHCl3) are presented below. Proton (1H) NMR spectra are a 4-scan average, with a time per scan of 0.75 s and 6 s recycle delay between pulses.




According to quantum mechanics, any nucleus is magnetically active if it possess a nonzero angular moment, P, which gives rise to a nuclear magnetic moment, µ, capable of interacting with an external magnetic field (Eq. 1).
(1) µ = γP
The magnetogyric ratio, γ, is the ratio of magnet moment to angular momentum. It relates the magnetic resonance (MR) frequency of a nuclide and the strength, or sensitivity of response of interaction of the nuclide when it is subjected to an external magnetic field. The 1H nucleus has the largest γ value (26.752 107 rad T-1 s-1) of stable isotopes on the NMR periodic table, making it the most sensitive to nuclear resonance excitation. The 19F nuclide comes next with a high magnetogyric ratio (25.18 107 rad T-1 s-1) at 94% of 1H, and has the advantage of 100% natural abundance. In combination, the result is a high relative sensitivity of 83% for fluorine.
With a dedicated Thermo Scientific™ picoSpin™ 45 19F NMR spectrometer, measuring19F NMR spectra in a bench-top instrument is as easy as acquiring proton spectra from the picoSpin™ 45 1H NMR spectrometer. A dedicated 19F spectrometer is tuned to the fluorine Larmor frequency (42.4 MHz) to yield the highest sensitivity for this nuclide. This application note presents 19F NMR spectra acquired from highly fluorinated small organic compounds, demonstrating the wealth of spectral information obtained from a bench-top picoSpin™ 45 19F NMR spectrometer.





Sample temperature measurement
Knowing the temperature of a sample within the RF coil of an NMR spectrometer is important when conducting kinetics or reaction monitoring experiments. Measuring the temperature of an NMR sample can be accomplished by direct methods, such as placing a temperature probe within the sample, or by monitoring the chemical shift dependence on sample temperature. The microbore capillary probe and magnet design of the Thermo Scientific picoSpin 45 NMR spectrometer precludes the possibility of using a direct method. However, in molecules like methanol and ethylene glycol, the chemical shift of the hydroxyl proton (OH) is strongly dependent on the extent of hydrogen bonding present. As the sample temperature is changed so too is the amount of hydrogen bonding, thus affecting the amount of shielding the nucleus experiences and resulting in changes in observed chemical shift. At low temperatures, where more hydrogen bonding is present in the sample, a downfield shift of the hydroxyl signal is observed while the chemical shift of the aliphatic signal remains unaffected. The chemical shift temperature probe method is commonly used in NMR and has been well studied by Van Geet and others.1,2,3,4
By using a chemical shift thermometer we are able to independently determine the temperature of methanol (CH3OH) and ethylene glycol (HOCH2CH2OH) samples within the RF coil of the capillary probe and make comparisons to thermistor sensor readings of the magnet temperature (as displayed on the Temperature page of the picoSpin-45 NMR spectrometer software). By this method we can generate temperature calibration curves for the displayed magnet temperature over the full operating temperature range of the picoSpin 45 NMR spectrometer.
All spectra were acquired from neat, reagent grade samples of methanol and ethylene glycol dried over calcium sulfate, using a 90 degree pulse angle and a 10 s T1 recovery delay; all spectra are the average of 16 scans. Spectra were obtained for six different magnet set-point temperatures and at 5 degree increments in the range of 20-45 °C.
Figure 1 shows the chemical shift dependence of the OH signal in methanol on varying sample temperature. At high magnet temperature (45 °C) the hydroxyl signal, experiencing less hydrogen bonding, appears upfield at δ4.5 whereas at the lower temperature limit (20 °C) the hydroxyl protons resonate further downfield (δ5.15); the CH3 appears at δ3.45.

The chemical shift dependence on temperature, derived originally by Van Geet1,2 for methanol at 60 MHz, is a quadratic function over the temperature range of the initial study (-53 – 57 °C) and is presented here in generalized form (Eq. 1), allow for scaling to different magnetic field strengths.
(1) T(°C) = 129.85 – (29.46/Tx) |∆ν| – (23.832/Tx2) ∆v2
Here Tx is the transmit frequency of the RF coil in MHz, T is the sample temperature in Celsius, and ∆ν is the frequency separation of the hydroxyl (OH) and methyl (CH3) groups in Hz. Although Equation 1 describes a quadratic function, the quadratic term is sufficiently small such that over the experimental temperature range of 25°C the data from Figure 1 can be fitted to a straight line as described by Equation 2.
(2) T(°C) = 166.19 – 2.0234 ∆ν

Like methanol, the response to changes in hydrogen bonding in ethylene glycol upon changing sample temperature is manifest in the chemical shift behavior of the OH signal. In Figure 2 the methylene resonance appears centered at δ4.0, while the hydroxyl signal shifts from a high temperature chemical shift value of δ5.4 to a low temperature downfield value of δ5.75. Van Geet found the downfield ‘walk’ of the hydroxyl signal with decreasing temperature for ethylene glycol to be nearly perfectly linear over a 100 degree temperature range (37-137 °C), and thus approximated this behavior by a linear function.2
(3) T(°C) = 192.85 – (101.64/Tx) ∆ν
The experimental data from Figure 2 demonstrates a similar linear response to changes in sample temperature. A fit of the chemical shift separation between OH and CH2plotted against magnet sensor temperature yields.
(4) T(°C) = 177.84 – 2.0709 ∆ν ,
where ∆ν is the frequency separation of the hydroxyl (OH) and methyl (CH2) groups in Hz. Equation 4 shows good agreement with Van Geet’s equation (3).

The relationship between the magnet temperature sensor reading displayed on the Temperature page of the picoSpin-45 NMR spectrometer software page and the observed chemical shift between the aliphatic and hydroxyl proton signal of the chemical probes can be seen in Figure 3. The error bars represent the observed error between the displayed magnet temperature and the temperature calculated from the difference in chemical shifts. The displayed and calculated temperatures show agreement to within 1 °C, demonstrating the accuracy of the picoSpin 45 spectrometer’s temperature monitoring sensor.
References
1 Van Geet, A. L. Anal. Chem., 1970, 42, 679-680.
2 Van Geet, A. L. Anal. Chem., 1968, 40, 2227-2229.
3 Raiford, D.S.; Fisk, C. L.; Becker. E. D. Anal. Chem. 1979, 51, 2050-2051.
4 Sikorski, W. H.; Sanders, A. W.; Reich, H. J. Magn. Reson. Chem.1998, 36, S118-S124.
Spectroscopy, elemental, and isotope analysis resource library
Access a targeted collection of application notes, case studies, videos, webinars and white papers covering a range of applications for Fourier Transform infrared spectroscopy, Near-infrared spectroscopy, Raman spectroscopy, Nuclear Magnetic Resonance, Ultraviolet-Visible (UV-Vis) spectrophotometry, X-Ray Fluorescence, and more.
